τάφος Αμφίπολης

Τάφος στον Κορινό Πιερίας σε σύγκριση με τον τάφο στην Αμφίπολη.Οι ανασκαφές έγιναν την εποχή του Ναπολεόντα στην περιοχή αλλά σταμάτησαν  με τον φόβο της ελονοσίας.Σχέδιο του τάφου του «Heuzey’s » στον Κορινό της Πύδνας. Οι Αιγές, ήταν η πρωτεύουσα του μακεδονικού βασιλείου το οποίο κυβερνούσε η δυναστεία των Αργεαδών από το 650 π.Χ. Όταν αρχαιολόγοι είχαν δείξει ενδιαφέρον για τους λόφους γύρω από την Βεργίνα ήδη από το 1850 υποψιαζόμενοι ότι μπορεί να ήταν ταφικά μνημεία, τότε άρχισαν οι ανασκαφές, το έτος 1861 υπό την επιτήρηση του Γάλλου αρχαιολόγου Leon Heuzey, ο οποίος υποστηριζόταν από τον αυτοκράτορα Ναπολέοντα Γ'. Τότε βρέθηκαν τμήματα του βασιλικού ανακτόρου. Παρ' όλα αυτά οι ανασκαφές σταμάτησαν για τον κίνδυνο της ελονοσίας. Τότε βρέθηκε και ο εν λόγω τάφος και για αυτό τον ονομάζουν έτσι.)

Αρχιτεκτονικά, στον τάφο στην Πύδνα, η πρόσοψη του δρόμου είναι απλή, και το υπέρθυρο και τα σκαλοπάτια κλίμακας είναι κατασκευασμένα από πωρόλιθο. Αυτή η μέθοδος, με πωρόλιθο, εφαρμόζεται επίσης για να σφραγίσει την είσοδο στον δρόμο εντός του τάφου. Παρά το γεγονός ότι η είσοδος στον δρόμο είναι 40 εκατοστά φαρδύτερη από την πρόσοψη του τάφου και ήταν ορατή στο κοινό κατά τη διάρκεια ταφικών τελετών, η πρόσοψη στην είσοδο του δεύτερου θαλάμου φέρει όλο τον αρχιτεκτονικό διάκοσμο. 







πρώτη απεικόνιση του τάφου(9/09/2014)


Αποκαλύφθηκαν πλήρως οι μαρμάρινες Σφίγγες που βρέθηκαν στον Τύμβο Καστά στην Αμφίπολη. Παράλληλα, βρέθηκε τμήμα από τη ράχη του Λέοντος, καθώς και μικρό τμήμα της ανωδομής του μνημείου από τις ανασκαφές που διεξάγει η ΚΗ΄ Εφορεία Προϊστορικών και Κλασικών Αρχαιοτήτων στην περιοχή, σύμφωνα με ανακοίνωση του υπουργείου Πολιτισμού και Αθλητισμού.

Συγκεκριμένα, η ανακοίνωση αναφέρει τα εξής: «Με την αφαίρεση, μέχρι στιγμής, των έντεκα λίθων από τον τοίχο σφράγισης, αποκαλύφθηκαν εξ ολοκλήρου οι Σφίγγες από μάρμαρο Θάσου. Το ύψος των αγαλμάτων είναι 1,45 μ. Το συνολικό ύψος με τις κεφαλές υπολογίζεται ότι θα έφτανε τα δύο μέτρα περίπου. Στους κορμούς, τους, που είναι δουλεμένοι με ψιλό ντισιλίδικο, αποτυπώνεται η πλαστικότητα και η λεπτοδουλειά των γλυπτών της τελευταίας εικοσιπενταετίας του 4ου π.Χ. αιώνα. Κατά τη διάρκεια των εργασιών βρέθηκαν τμήματα των πτερών των Σφιγγών -που ήταν ένθετα στους κορμούς- και τα οποία επιτρέπουν την πλήρη αποκατάστασή τους. Βρέθηκε, επίσης, τμήμα από τη ράχη του αγάλματος του Λέοντος της Αμφίπολης. Τόσο οι Σφίγγες, όσο και ο Λέων φαίνεται να προέρχονται από το ίδιο εργαστήριο. Με την αφαίρεση των χωμάτων, εμφανίστηκε, επίσης, μικρό τμήμα της ανωδομής του μνημείου, που φέρει ίχνη κόκκινου και μπλε χρώματος, σε δυο αποχρώσεις αντίστοιχα. Οι εργασίες συνεχίζονται στη στάθμη του εσωρραχίου της θόλου, με τη στερέωση και στήριξη των λίθων της καθώς και την αφαίρεση των χωμάτων».(πηγή:http://www.kathimerini.gr/780446/article/epikairothta/ellada/plhrhs-apokalyyh-gia-tis-sfigges-ths-amfipolhs)

πηγή:Αρχαιογνώμων

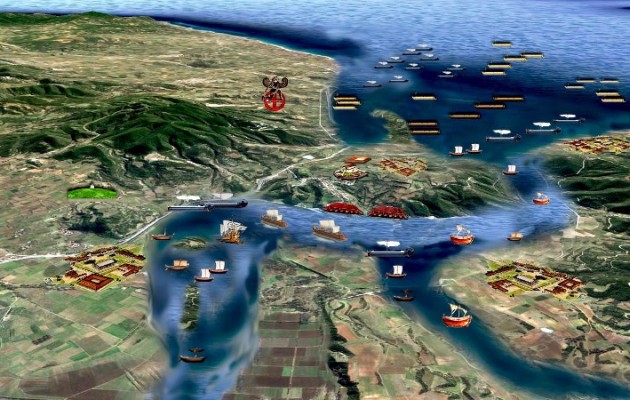
Η γεωμορφολογία της περιοχής έχει αλλάξει ωστόσο ριζικά από την αρχαιότητα λόγω της διαφοροποίησης της κοίτης του Στρυμόνα και της αποξήρανσης της λίμνης Κερκινίτιδας.

Οι αρχαίες πηγές μιλούν όμως για τα ωραία αγκυροβόλια αυτής της λίμνης, η οποία συνδεόταν με το ποτάμι. Ένα ποτάμι πλωτό, που παρείχε τη δυνατότητα στα πλοία να φθάνουν ως την Αμφίπολη. Όσο για τον τύμβο με τον Λέοντα, βρισκόταν ακριβώς μπροστά στη λίμνη.

Η κατασκευή του ταφικού μνημείου που έφερε στο φως η αρχαιολογική σκαπάνη εκτιμάται ότι διήρκεσε περί τα δύο χρόνια.

Την εποχή που κατασκευάστηκε το ταφικό μνημείο, ανάμεσα στα 325-300 π.Χ. -δηλαδή περί τα τέλη του 4ου αιώνα π.Χ.- ο Στρυμόνας ήταν πλωτός και είχε έκταση που μπορούσε να συγκριθεί με αυτή του Νείλου στην Αίγυπτο. Άλλωστε μέρος του μακεδονικού στόλου απέπλευσε για την εκστρατεία στην Ασία από την Αμφίπολη.

ανάκτορο Γαλέριου Θεσ/νικης

Οι φωτογραφίες  που ακολουθούν είναι τρισδιάστατες ψηφιακές αναπαραστάσεις του Γαλεριανού ανακτόρου στη Θεσ/νικη.Έτσι ήταν η πόλη πριν από 1.500 χρόνια.

ανακοίνωση για μαθηματικά

http://3dim-evosm.web.auth.gr/archives/1228
Μπορείτε να δείτε την ανακοίνωση για τον διαγωνισμό μαθηματικών που έγινε στο 3ο Πειραματικό Σχολείο Ευόσμου.Καλά να περνάτε.

πειράματα για την τάξη

http://blogs.auth.gr/koumaras/files/2014/04/2.pdf

Πείραμα 1: Το αναποδογυρισμένο γεμάτο με νερό μπουκάλι που δε χύνεται.

Τι χρειάζεσαι: Ένα ποτήρι, ένα μεγάλο γυάλινο (ή από σκληρό πλαστικό) μπουκάλι νερού, νερό.

 Τι θα κάνεις: Τοποθέτησε ένα άδειο ποτήρι όρθιο με το στόμιό του προς
τα πάνω. Γέμισε το μπουκάλι με νερό και αναποδογύρισέ το πάνω στο ποτήρι
ώστε το στόμιο του μπουκαλιού να είναι μέσα στο ποτήρι. Κράτησε το μπου-
κάλι σε αυτή τη θέση.

Τι θα δεις: Αρχικά χύνεται λίγο νερό από το μπουκάλι στο ποτήρι και
όταν το στόμιο του μπουκαλιού βρεθεί μέσα στο νερό, τότε το νερό σταματάει
να χύνεται από το μπουκάλι στο ποτήρι.

Ερμηνεία: Η ατμοσφαιρική πίεση εξισορροπεί την πίεση που οφείλεται
στο νερό που βρίσκεται μέσα στο μπουκάλι και στον εγκλωβισμένο μέσα στο
μπουκάλι αέρα. Σημειώνουμε ότι το μεγαλύτερο μέρος της πίεσης μέσα στο
μπουκάλι οφείλεται στον εγκλωβισμένο στο μπουκάλι αέρα. Η ατμοσφαιρική
πίεση είναι κανονικά ίση 1033 cm στήλης νερού (76 cm στήλης υδραργύρου).


Παρατήρηση: Αν χρησιμοποιήσεις πλαστικό μπουκάλι με μαλακά τοιχώματα υπάρχει κίνδυνος να παραμορφωθεί όταν το αναποδογυρίσεις και να αποτύχει το πείραμα.

Πείραμα 2: Το αναποδογυρισμένο γεμάτο με νερό ποτήρι που δε χύνεται. 

Τι χρειάζεσαι: Ένα ποτήρι, το 1/4 από ένα φύλλο χαρτιού φωτοτυπίας (ή καλύτερα ένα λεπτό χαρτόνι αντίστοιχου μεγέθους), νερό, μια λεκάνη. 

Τι θα κάνεις: Γέμισε το ποτήρι με νερό. Γέμισέ το σιγά και προσεχτικά μέχρι να δεις την επιφάνεια του νερού  να είναι πάνω από τα χείλη του ποτηριού. Πίεσε απαλά με την παλάμη το χαρτί πάνω στην επιφάνεια του νερού και κρατώντας εκεί την παλάμη σου αναποδογύρισε το ποτήρι πάνω από την λεκάνη.

Πάρε το χέρι σου (η λεκάνη χρειάζεται για την περίπτωση αποτυχίας ώστε να μη γεμίσεις τον τόπο νερά) 

Τι θα δεις: Το φύλλο του χαρτιού δεν φεύγει από τα χείλη του ποτηριού και έτσι το νερό δε χύνεται. 

Ερμηνεία: Λόγω της ατμοσφαιρικής πίεσης προκαλείται δύναμη στην εξωτερική επιφάνεια του χαρτιού η οποία συγκρατεί το νερό και το χαρτί. 

Σημειώσεις. 1) Προσοχή: Το χαρτί να είναι τελείως επίπεδο, σε διαφορετική περίπτωση περνάει αέρας μεταξύ του χαρτιού και της επιφάνειας του νερού με συνέπεια το νερό να χύνεται. Χαρτί που χρησιμοποιήθηκε ήδη στο πείραμα μπορεί να δημιουργήσει προβλήματα αν χρησιμοποιηθεί και δεύτερη φορά (ελέγχεις αν έχει παραμορφώσεις, αν «ζάρωσε» από το βρέξιμο) 2) Το χαρτί να μην έχει πολύ μεγαλύτερες διαστάσεις από τις απαιτούμενες να καλύψουν καλά το στόμιο του ποτηριού, σε διαφορετική περίπτωση το χαρτί λυγίζει από το βάρος του και υπάρχει περίπτωση να μπει αέρας ανάμεσα στο χαρτί και την επιφάνεια του νερού. 3) Μπορείς στην αρχή να δείξεις ότι με άδειο το ποτήρι το χαρτί φεύγει από το στόμιο του ποτηριού όταν το αναποδογυρίσεις, ενώ δεν φεύγει όταν το ποτήρι είναι γεμάτο με νερό. 

Από αυτά τα πειράματα θα ήθελα να διαλέξετε και να κάνετε στην τάξη ,στο επόμενο μάθημα φυσικής.

Επίσης θα έχετε φέρει ένα πλαστικό μπουκάλι νερού κομμένο στη μέση (θα το κάνουν οι γονείς σας)

και το καπάκι του.

 καλή επιτυχία

Η γιορτή της Αναλήψεως

 Η εορτή της Αναλήψεως, σαράντα ημέρες μετά την Ανάσταση, σηματοδοτεί το τέλος της επίγειας παρουσίας του Κυρίου μας και την άνοδό Του στους ουρανούς, πλησίον του Θεού και Πατρός. Ο Χριστός όμως δεν επιστρέφει από εκεί που ξεκίνησε πριν την Σάρκωσή Του, ως Θεός μόνο. Πλέον, ανεβάζει στους ουρανούς την ανθρώπινη φύση και ξαναδίδει στον άνθρωπο αυτό που του έλειπε:  την δυνατότητα συνεχούς κοινωνίας με το Θεό, τη δυνατότητα υπερβάσεως της αμαρτίας και του θανάτου, τη δυνατότητα της σωτηρίας, της θεώσεως και της λυτρώσεως. Και αυτή η σωτηρία δεν υπάρχει πλέον ως προσδοκία ή ως επιθυμία, αλλά ως βεβαιότητα.
 Ο Κύριός μας επισφραγίζει την Ανάσταση, την διδασκαλία Του, τις υποσχέσεις Του με την Ανάληψή Του. Συνοδευόμενος από τους Αγγέλους, εν νεφέλη φωτεινή, ανεβαίνει εις ουρανούς. Δείχνει στους μαθητές Του, αλλά και σε κάθε χριστιανό ότι τα πάντα γι’ Αυτόν είναι δυνατά. Το επίγειο έργο Του ετελείωσε. Το αφήνει τώρα παρακαταθήκη στους μαθητές, αλλά και σε όλους εμάς που πιστεύουμε σ’ Αυτόν. Και Εκείνος μας περιμένει, έχοντας δώσει στον καθένα την δυνατότητα να νικήσει την φύση του, να ανεβούμε πνευματικά εις ύψος νοητόν, σε κοινωνία και σχέση μαζί Του, να αφήσουμε την όποια προσκόλληση στην καθημερινότητα της ζωή μας και να ζητήσουμε και την δική μας ανάληψη πλησίον Του. Όχι αποκόπτοντας τον εαυτό μας από τη ζωή μας, αλλά δίδοντάς της άλλο νόημα.
Η βεβαιότητα της πίστεως ανεβάζει τον άνθρωπο εις ουρανούς. Δίδει δόξα, τιμή και ελπίδα στον πιστό. Προσφέρει γνήσια χαρά, που αγιάζει τη ζωή μας. Και δια της σχέσεως με τον Αναληφθέντα Κύριό μας εν τη Εκκλησία, επαναφέρει το «αρχαίον κάλλος» στην φύση μας. Δεν είμαστε μόνοι μας. Δεν καταλήγει η ζωή μας στον θάνατο. Μπορούμε να νικήσουμε την ματαιότητα και την φθαρτότητα. Ο ίδιος ο Κύριός μας, δια της Αναλήψεώς Του, μας δίδει αυτή την βεβαιότητα. Και η ευλογία βιώνεται κάθε φορά που η Εκκλησία μας τελεί τα μυστήρια της, εορτάζει τους Αγίους της, υπενθυμίζει τον λόγο του Κυρίου στο Ευαγγέλιο. Αυτή την βεβαιότητα ουδείς την εγκρέμισε στους αιώνες. Και κάθε φορά που ο καθένας μας τη ζει, ανέρχεται πλησίον του Θεού. Δια του Αναληφθέντος Κυρίου μας. 

Tου Σεβ. Μητροπολίτου Κερκύρας, Παξών και Διαποντίων Νήσων κ. Νεκταρίου

Βυζαντινός περίπατος

http://www.slideboom.com/presentations/1013347/%CE%92%CF%85%CE%B6%CE%B1%CE%BD%CF%84%CE%B9%CE%BD%CF%8C%CF%82--%CF%80%CE%B5%CF%81%CE%AF%CF%80%CE%B1%CF%84%CE%BF%CF%82?pk=9e31-8350-5e1a-ddb1-7dc1-7df6-085c-c618

https://www.dropbox.com/sh/k4g3m2f7dsiqkti/AAAG_LDFEgMhaPCrilOmO6k3a?n=121188221

https://www.dropbox.com/s/wyrldyf7w7qtpv5/%CE%92%CF%85%CE%B6%CE%B1%CE%BD%CF%84%CE%B9%CE%BD%CF%8C%CF%82%20%CE%A0%CE%B5%CF%81%CE%AF%CF%80%CE%B1%CF%84%CE%BF%CF%82.ppt

φυσική -πεπτικό σύστημα

http://kaskas.mysch.gr/images/flash/digestiveactivity.swf

ερωτηματολόγιο

Ερωτηματολόγιο για την Τηλεόραση(21-05-2014)Ε2 Δ.Σ.Λαγυνών

η οδοντόβουρτσα της Ειρήνης μας λέει...

Γειά σας,είμαι η οδοντόβουρτσα της Ειρήνης .Είμαι εχθρός με τα μικρόβια και φίλη με την καθαριότητα και την καλή υγιεινή του στόματος.Η Αρετή μας έδειξε πώς θα το κάνουμε σωστά.

1.Κυκλικές κινήσεις ,που να πιάνει και το ούλο.

2.Όχι βιαστικό βούρτσισμα.

3.Βουρτσίζω όλα τα δόντια.

Είναι δύσκολο; Αποφασίστε ή γερά δόντια και καλή υγιεινή  στο στόμα μου ή χαλασμένα δόντια με πολλά έξοδα και  πόνο.

Παλαιοντολογία

http://www.bbc.co.uk/schools/primaryhistory/famouspeople/mary_anning/




Το σκίτσο αυτό αναπαριστά σε τομή τα υπολείμματα του ελέφαντα σε οικόπεδα στην περιοχή Αμπέλια, καθώς και τον τρόπο που βρέθηκαν στην επιφάνεια του εδάφους, μετά τη διάβρωση και απομάκρυνση από τα νερά της βροχής των στρωμάτων που τα κάλυπταν(από το Μουσείο Φυσικής Ιστορίας Γρεβενών. http://www.mfi-miliasgrevenon.gr/site/

τηλεόραση

το κεφάλαιο για την τηλεόραση από τον κ.Αρβανιτίδη
http://users.sch.gr/theoarvani/mathimata/etaxi/glossa15.html
φωνή και διάθεση ρημάτων
http://users.sch.gr/ipap/Ellinikos%20Politismos/Yliko/Theoria%20Nea/diathesi-rim-NE.htm

κλίμακα μαθηματικά

Ζωγραφίζοντας το σπίτια του χωριού μας με κλίμακα 1/100 και 1/200. 

Στο σπίτι στο μύλο η κλίμακα 1/100 ,στο σπίτι της κ.Όλγας 1/100 ,στον τοίχο της πλατείας με 1/200 και τον γέρο πλάτανο με 1/100.Στο καφενείο  καθόταν κάποιοι και  μας πρότειναν να τρώμε περισσότερο,αλλά η τροφή δεν μπορεί να είναι στον άνθρωπο μόνο υλική αλλά επιβάλλεται να είναι και πνευματική.

το σπίτι δίπλα στον μύλο

θρανία ο δρόμος 

το σπίτι της κυρα -Όλγας

σε απόλυτη κλίμακα

σε απόλυτη κλίμακα

σε απόλυτη κλίμακα

η πόρτα αυτή άραγε πόσα είδε;

στον πλάτανο

στον πλάτανο 

τέχνη βυζαντινή

Την περίοδο των τελευταίων αυτοκρατόρων του Βυζαντίου ,των Παλαιολόγων δημιουργήθηκαν δυο σχολές βυζαντινής τεχνοτροπίας:η βυζαντινή και η κρητική.Τα χαρακτηριστικά τους μπορείς να τα βρεις στον παρακάτω σύνδεσμο.Τι τεχνοτροπίας είναι οι αγιογραφίες  στον Ι.Ν.Αγίου Νικολάου Λαγυνών;

http://www.imma.edu.gr/macher/subjects/athos/art.html#toc003

Επίσκεψη στην έκθεση ζωγραφικής  στα Λαγυνά από το Ε1 και το Ε2 .Ευχαριστούμε τον κ.Λελιούδη για την παρουσίαση που μας έκανε για τα έργα των παιδιών αλλά και την αξία των εικαστικών στη ζωή μας.

γυναίκες επιστημόνισσες

http://www.pi.ac.cy/pi/files/epimorfosi/isotita_fylou/dimgymn/arxeia/epistimi/Istoselides/Gunaikes_Viologoi.pdf

Σαν σήμερα, στις 12 Μαϊου 1910 γεννήθηκε η μεγάλη βρετανίδα βιοχημικός Dorothy Hodgkin. 
Για τις καινοτόμες τεχνικές που εφάρμοσε καθ'όλη σχεδόν την επιστημονική της σταδιοδρομία αλλά και τις επιστημονικές της ανακαλύψεις βραβεύτηκε με Νόμπελ Χημείας το 1964...
Από πολύ νωρίς, από το 1921 όταν φοιτούσε σε σχολείο στην Αγγλία, ήταν πλέον είναι για το τι ήθελε να κάνει στη ζωή της: αποφάσισε να αφοσιωθεί στη χημεία, με την οποία ήρθε σε πιο στενή επαφή στα σχολικά της χρόνια, αν και η αρχαιολογία ποτέ δεν έπαψε να την ενδιαφέρει, καθώς ο πατέρας της ήταν αρχαιολόγος, και η μητέρα της η βοηθός του.
Το 1934, ο καθηγητής της στο Κέιμπριτζ κατάφερε να απαθανατίσει σε ακτινογραφία για πρώτη φορά στην ιστορία της επιστήμης την κρυσταλλική δομή μιας πρωτεΐνης, με τη βοηθό του Χότζκιν να κάνει όλες τις απαραίτητες αναλύσεις. 
Μια από τις πρώιμες επιτυχίες της Χότζκιν ήταν η διαλεύκανση της μοριακής δομής της χοληστερόλης, ενώ αργότερα θα δούλευε πυρετωδώς πάνω στην πενικιλίνη: το 1942 δημοσιεύει τα αποτελέσματα της έρευνάς της, αποκαλύπτοντας τη χημική δομή της πενικιλίνης και ανοίγοντας έτσι τον δρόμο για τη συνθετική παρασκευή της!

ασκήσεις γλώσσας και μαθηματικών

Ένας νεαρός σηκώνεται το πρωί και πηγαίνει στην τουαλέτα για να πλύνει τα δόντια του. Εκεί βρίσκει την καινούρια οδοντόκρεμα «Φαφουτέξ».

– Για να δούμε και αυτή την οδοντόκρεμα, άκουσα πως είναι διαφορετική από τις άλλες. Μου είπαν ότι λύνει για πάντα το πρόβλημα του βουρτσίσματος των δοντιών!

Την ανοίγει και τη βάζει στην οδοντόβουρτσα. Αρχίζει να βουρτσίζει τα δόντια του και βάζει τις φωνές:

– Τα δόντια μου, τα δόντια μου, χάθηκαν!

Τότε ακούγεται η φωνή του εκφωνητή να λέει:

– Νέα καταπληκτική οδοντόκρεμα «ΦΑΦΟΥΤΕΞ», κάνει τα δόντια αόρατα!

• Σίγουρα εσείς μπορείτε να φτιάξετε μια πολύ καλύτερη. Εμπρός λοιπόν!

  

τηλεταινία > _____________________________=_____________________________________________________

______________________________________________________________________________________________

   

http://photodentro.edu.gr/photodentro/mtpd_c03_melisses_pidx0016574/
3.μέλισσες
Μαθηματικά
http://users.sch.gr/vaskitsios/katsba/dim/d/ma8-symmigeis.htm



Γράψε τα προβλήματα στο τετράδιό σου .Μπορείς να τα λύσεις;
http://harlemcore13.blogspot.gr/2011/05/52.html

ιστορία

Ρώμη

Πάνθεον

Όλο το κεφάλαιο  28 της ιστορίας(3ο ΠΠΣ Ευόσμου)

http://3psevosmou.wix.com/e-experimental#!--/cvyu

Άλλοι ιστότοποι

Για ασκήσεις ιστορίας
http://online.eduportal.gr/a_online_istoria.htm
Για τις μαύρες τρύπες υπάρχει ανάρτηση στο Δ.Σ.Χολαργού (δεξιά και κάτω)
http://5dimcholarg.wordpress.com/%CF%80%CF%81%CE%BF%CE%B3%CF%81%CE%B1%CE%BC%CE%BC%CE%B1%CF%84%CE%B1-2/%CE%B5%CE%BA%CF%80%CE%B1%CE%B9%CE%B4%CE%B5%CF%85%CF%84%CE%B9%CE%BA%CE%BF-%CF%85%CE%BB%CE%B9%CE%BA%CE%BF/%CE%B1%CF%83%CE%BA%CE%AE%CF%83%CE%B5%CE%B9%CF%82-%CE%B9%CF%83%CF%84%CE%BF%CF%81%CE%AF%CE%B1%CF%82-on-line-%CE%B1%CF%80%CF%8C-%CE%B5%CE%BB%CE%BB%CE%B7%CE%BD%CE%B9%CE%BA%CE%AE-%CF%80%CF%8D%CE%BB%CE%B7/

FBonatsi

Στα Μαθηματικά, οι Αριθμοί Φιμπονάτσι είναι οι αριθμοί της παρακάτω ακέραιης ακολουθίας:

Εξ ορισμού, οι πρώτοι δύο αριθμοί Φιμπονάτσι είναι το 0 και το 1, και κάθε επόμενος αριθμός είναι το άθροισμα των δύο προηγούμενων.

Σε μαθηματικούς όρους, η ακολουθία F_n των αριθμών Φιμπονάτσι ορίζεται από τον αναδρομικό τύπο:

με  και . ^[1]

Η Ακολουθία Φιμπονάτσι ονομάστηκε έτσι από τον Λεονάρντο της Πίζας, γνωστό και ως Φιμπονάτσι. Το βιβλίο του Φιμπονάτσι, το 1202, με τίτλο Liber Abaci, εισήγαγε την ακολουθία στα Μαθηματικά της Δυτικής Ευρώπης.(Βικιπαίδεια)

Τα φυτά δε γνωρίζουν για την ακολουθία Fibonacci, απλά μεγαλώνουν με τον πιο πρόσφορο και αποδοτικό τόπο. Όμως η ακολουθία κάνει την εμφάνισή της στη διάταξη των φύλων γύρω από το μίσχο. Εμφανίζεται επίσης στην ανάπτυξη των βελόνων αρκετών ειδών ελάτου, καθώς επίσης και στη διάταξη των πετάλων στις μαργαρίτες και τα ηλιοτρόπια. Μερικά κωνοφόρα δένδρα παρουσιάζουν τη σειρά αριθμών στη δομή της επιφάνειας των κορμών τους, ενώ τα φοινικόδενδρα στους δακτυλίους των κορμών τους.

Όμως πώς προκύπτει αυτή η διάταξη, αυτή η συμμετρία σε σχέση με την ακολουθία; Στην περίπτωση του φυλλώματος μπορεί να σχετίζεται με τη μεγιστοποίηση του χώρου που είναι διαθέσιμος για την ανάπτυξη κάθε φύλλου ή το φώς πρέπει να πέφτει πάνω στο κάθε φύλλο. Η φύση προφανώς δεν προσπαθεί να χρησιμοποιήσει την ακολουθία Fibonacci, αυτή εμφανίζεται ώς το δευτερεύον αποτέλεσμα μιας πολύ βαθύτερης φυσικής διαδικασίας.

Ένα άλλο παράδειγμα είναι το ίδιο το ανθρώπινο χέρι: κάθε άνθρωπος έχει 2 χέρια, κάθε ένα από τα οποία έχει 5 δάκτυλα, κάθε δάκτυλο αποτελείται από 3 τμήματα που χωρίζονται από 2 αρθρώσεις. Όλοι αυτοί οι αριθμοί ανήκουν στην ακολουθία Fibonacci.

Η γνώση του αριθμού φ και του χρυσού ορθογωνίου ανάγεται στους αρχαίους Έλληνες οι οποίοι βάσισαν πάνω τους το πιο γνωστό έργο τέχνης: ο Παρθενώνας είναι γεμάτος από χρυσά ορθογώνια. Οι μαθητές του μαθηματικού και φιλοσόφου Πυθαγόρα έφταναν στο σημείο να θεωρούν τη χρυσή αναλογία, θεόπνευστη.

Αργότερα ο Leonardo Da Vinci ζωγράφισε το πρόσωπο της Mona Lisa ώστε αυτό να χωράει τέλεια σε ένα χρυσό ορθογώνιο και δόμησε τον υπόλοιπο πίνακα γύρω από το πρόσωπο χωρίζοντάς τον επίσης σε χρυσά ορθογώνια.

Ο Mozart διαίρεσε μεγάλο αριθμό από τις σονάτες του σε δύο μέρη, η χρονική αναλογία των οποίων αντιστοιχεί στη χρυσή τομή, τον αριθμό φ, αν και υπάρχει σημαντική διχογνωμία για το κατά πόσο αυτό έγινε σκόπιμα. Πιο πρόσφατα ο Ούγγρος συνθέτης Bela Bartok και ο Γάλλος αρχιτέκτονας Le Corbusier χρησιμοποίησαν σκόπιμα τη χρυσή αναλογία στα έργα τους. Όμως ακόμα και ο χριστιανικός σταυρός αποτελείται από δύο κάθετες μεταξύ τους γραμμές με την αναλογία ανάμεσα στην κατακόρυφη και την οριζόντια να μην είναι άλλη από τον αριθμό φ.
Ακόμη και σήμερα η χρυσή αναλογία απαντάται σε πλήθος αντικείμενα φτιαγμένα από τον άνθρωπο. Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα το σχήμα της οποίας είναι ακριβώς αυτό.

Οι πολυάριθμες εμφανίσεις της χρυσής αναλογίας, και των χρυσών ορθογωνίων στην τέχνη, είναι αντικείμενο συζητήσεων και ερευνών μεταξύ των ψυχολόγων για το κατά πόσο οι άνθρωποι αντιλαμβάνονται το χρυσό ορθογώνιο για παράδειγμα, ώς πιο όμορφο και αρμονικό σχήμα από οποιοδήποτε άλλο ορθογώνιο. Το 1995 ο καθηγητής Christopher Green του Πανεπιστημίου York στο Toronto, σε ένα άρθρο του στο περιοδικό Perception παρουσιάζει τα αποτελέσματα μιας σειράς πειραμάτων που δεν έδειξαν κάποια μετρήσιμη προτίμηση για το χρυσό ορθογώνιο, δεν παραλείπει όμως να αναφέρει ότι αρκετοί άλλοι συνάδελφοί του έχουν αντίστοιχα δεδομένα που υποδηλώνουν ακριβώς το αντίθετο, ότι δηλαδή υπάρχει μια τέτοια τάση.

Πέρα όμως από τα επιστημονικά δεδομένα η χρυσή αναλογία, ο αριθμός φ, περιβάλλεται από ένα πέπλο μυστηρίου, κυρίως γιατί εντυπωσιακές προσεγγίσεις του απαντώνται, εντελώς απρόσμενα σε ένα σωρό μέρη στη φύση. Ακόμα και μια τομή του ανθρώπινου DNA φαίνεται να ενσωματώνεται άψογα σε ένα χρυσό δεκάγωνο. Η χρυσή αναλογία και τα σχήματα που σχετίζονται με αυτή συνεχίζουν να κινούν το ενδιαφέρον των μαθηματικών, αλλά και των απλών ανθρώπων.
Πηγή: Άρθουρ Μπέντζαμιν: Η μαγεία της ακολουθίας Φιμπονάτσι