Στα Μαθηματικά, οι Αριθμοί Φιμπονάτσι είναι οι αριθμοί της παρακάτω ακέραιης ακολουθίας:
Εξ ορισμού, οι πρώτοι δύο αριθμοί Φιμπονάτσι είναι το 0 και το 1, και κάθε επόμενος αριθμός είναι το άθροισμα των δύο προηγούμενων.
Σε μαθηματικούς όρους, η ακολουθία Fn των αριθμών Φιμπονάτσι ορίζεται από τον αναδρομικό τύπο:
Η Ακολουθία Φιμπονάτσι ονομάστηκε έτσι από τον Λεονάρντο της Πίζας, γνωστό και ως Φιμπονάτσι. Το βιβλίο του Φιμπονάτσι, το 1202, με τίτλο Liber Abaci, εισήγαγε την ακολουθία στα Μαθηματικά της Δυτικής Ευρώπης.(Βικιπαίδεια)
Τα φυτά δε γνωρίζουν για την ακολουθία Fibonacci, απλά μεγαλώνουν με τον πιο πρόσφορο και αποδοτικό τόπο. Όμως η ακολουθία κάνει την εμφάνισή της στη διάταξη των φύλων γύρω από το μίσχο. Εμφανίζεται επίσης στην ανάπτυξη των βελόνων αρκετών ειδών ελάτου, καθώς επίσης και στη διάταξη των πετάλων στις μαργαρίτες και τα ηλιοτρόπια. Μερικά κωνοφόρα δένδρα παρουσιάζουν τη σειρά αριθμών στη δομή της επιφάνειας των κορμών τους, ενώ τα φοινικόδενδρα στους δακτυλίους των κορμών τους.
Όμως πώς προκύπτει αυτή η διάταξη, αυτή η συμμετρία σε σχέση με την ακολουθία; Στην περίπτωση του φυλλώματος μπορεί να σχετίζεται με τη μεγιστοποίηση του χώρου που είναι διαθέσιμος για την ανάπτυξη κάθε φύλλου ή το φώς πρέπει να πέφτει πάνω στο κάθε φύλλο. Η φύση προφανώς δεν προσπαθεί να χρησιμοποιήσει την ακολουθία Fibonacci, αυτή εμφανίζεται ώς το δευτερεύον αποτέλεσμα μιας πολύ βαθύτερης φυσικής διαδικασίας.
Ένα άλλο παράδειγμα είναι το ίδιο το ανθρώπινο χέρι: κάθε άνθρωπος έχει 2 χέρια, κάθε ένα από τα οποία έχει 5 δάκτυλα, κάθε δάκτυλο αποτελείται από 3 τμήματα που χωρίζονται από 2 αρθρώσεις. Όλοι αυτοί οι αριθμοί ανήκουν στην ακολουθία Fibonacci.
Η γνώση του αριθμού φ και του χρυσού ορθογωνίου ανάγεται στους αρχαίους Έλληνες οι οποίοι βάσισαν πάνω τους το πιο γνωστό έργο τέχνης: ο Παρθενώνας είναι γεμάτος από χρυσά ορθογώνια. Οι μαθητές του μαθηματικού και φιλοσόφου Πυθαγόρα έφταναν στο σημείο να θεωρούν τη χρυσή αναλογία, θεόπνευστη.
Αργότερα ο Leonardo Da Vinci ζωγράφισε το πρόσωπο της Mona Lisa ώστε αυτό να χωράει τέλεια σε ένα χρυσό ορθογώνιο και δόμησε τον υπόλοιπο πίνακα γύρω από το πρόσωπο χωρίζοντάς τον επίσης σε χρυσά ορθογώνια.
Ο Mozart διαίρεσε μεγάλο αριθμό από τις σονάτες του σε δύο μέρη, η χρονική αναλογία των οποίων αντιστοιχεί στη χρυσή τομή, τον αριθμό φ, αν και υπάρχει σημαντική διχογνωμία για το κατά πόσο αυτό έγινε σκόπιμα. Πιο πρόσφατα ο Ούγγρος συνθέτης Bela Bartok και ο Γάλλος αρχιτέκτονας Le Corbusier χρησιμοποίησαν σκόπιμα τη χρυσή αναλογία στα έργα τους. Όμως ακόμα και ο χριστιανικός σταυρός αποτελείται από δύο κάθετες μεταξύ τους γραμμές με την αναλογία ανάμεσα στην κατακόρυφη και την οριζόντια να μην είναι άλλη από τον αριθμό φ.
Ακόμη και σήμερα η χρυσή αναλογία απαντάται σε πλήθος αντικείμενα φτιαγμένα από τον άνθρωπο. Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα το σχήμα της οποίας είναι ακριβώς αυτό.
Οι πολυάριθμες εμφανίσεις της χρυσής αναλογίας, και των χρυσών ορθογωνίων στην τέχνη, είναι αντικείμενο συζητήσεων και ερευνών μεταξύ των ψυχολόγων για το κατά πόσο οι άνθρωποι αντιλαμβάνονται το χρυσό ορθογώνιο για παράδειγμα, ώς πιο όμορφο και αρμονικό σχήμα από οποιοδήποτε άλλο ορθογώνιο. Το 1995 ο καθηγητής Christopher Green του Πανεπιστημίου York στο Toronto, σε ένα άρθρο του στο περιοδικό Perception παρουσιάζει τα αποτελέσματα μιας σειράς πειραμάτων που δεν έδειξαν κάποια μετρήσιμη προτίμηση για το χρυσό ορθογώνιο, δεν παραλείπει όμως να αναφέρει ότι αρκετοί άλλοι συνάδελφοί του έχουν αντίστοιχα δεδομένα που υποδηλώνουν ακριβώς το αντίθετο, ότι δηλαδή υπάρχει μια τέτοια τάση.
Πέρα όμως από τα επιστημονικά δεδομένα η χρυσή αναλογία, ο αριθμός φ, περιβάλλεται από ένα πέπλο μυστηρίου, κυρίως γιατί εντυπωσιακές προσεγγίσεις του απαντώνται, εντελώς απρόσμενα σε ένα σωρό μέρη στη φύση. Ακόμα και μια τομή του ανθρώπινου DNA φαίνεται να ενσωματώνεται άψογα σε ένα χρυσό δεκάγωνο. Η χρυσή αναλογία και τα σχήματα που σχετίζονται με αυτή συνεχίζουν να κινούν το ενδιαφέρον των μαθηματικών, αλλά και των απλών ανθρώπων.
Πηγή: Άρθουρ Μπέντζαμιν: Η μαγεία της ακολουθίας Φιμπονάτσι
Τα φυτά δε γνωρίζουν για την ακολουθία Fibonacci, απλά μεγαλώνουν με τον πιο πρόσφορο και αποδοτικό τόπο. Όμως η ακολουθία κάνει την εμφάνισή της στη διάταξη των φύλων γύρω από το μίσχο. Εμφανίζεται επίσης στην ανάπτυξη των βελόνων αρκετών ειδών ελάτου, καθώς επίσης και στη διάταξη των πετάλων στις μαργαρίτες και τα ηλιοτρόπια. Μερικά κωνοφόρα δένδρα παρουσιάζουν τη σειρά αριθμών στη δομή της επιφάνειας των κορμών τους, ενώ τα φοινικόδενδρα στους δακτυλίους των κορμών τους.
Όμως πώς προκύπτει αυτή η διάταξη, αυτή η συμμετρία σε σχέση με την ακολουθία; Στην περίπτωση του φυλλώματος μπορεί να σχετίζεται με τη μεγιστοποίηση του χώρου που είναι διαθέσιμος για την ανάπτυξη κάθε φύλλου ή το φώς πρέπει να πέφτει πάνω στο κάθε φύλλο. Η φύση προφανώς δεν προσπαθεί να χρησιμοποιήσει την ακολουθία Fibonacci, αυτή εμφανίζεται ώς το δευτερεύον αποτέλεσμα μιας πολύ βαθύτερης φυσικής διαδικασίας.
Ένα άλλο παράδειγμα είναι το ίδιο το ανθρώπινο χέρι: κάθε άνθρωπος έχει 2 χέρια, κάθε ένα από τα οποία έχει 5 δάκτυλα, κάθε δάκτυλο αποτελείται από 3 τμήματα που χωρίζονται από 2 αρθρώσεις. Όλοι αυτοί οι αριθμοί ανήκουν στην ακολουθία Fibonacci.
Η γνώση του αριθμού φ και του χρυσού ορθογωνίου ανάγεται στους αρχαίους Έλληνες οι οποίοι βάσισαν πάνω τους το πιο γνωστό έργο τέχνης: ο Παρθενώνας είναι γεμάτος από χρυσά ορθογώνια. Οι μαθητές του μαθηματικού και φιλοσόφου Πυθαγόρα έφταναν στο σημείο να θεωρούν τη χρυσή αναλογία, θεόπνευστη.
Αργότερα ο Leonardo Da Vinci ζωγράφισε το πρόσωπο της Mona Lisa ώστε αυτό να χωράει τέλεια σε ένα χρυσό ορθογώνιο και δόμησε τον υπόλοιπο πίνακα γύρω από το πρόσωπο χωρίζοντάς τον επίσης σε χρυσά ορθογώνια.
Ο Mozart διαίρεσε μεγάλο αριθμό από τις σονάτες του σε δύο μέρη, η χρονική αναλογία των οποίων αντιστοιχεί στη χρυσή τομή, τον αριθμό φ, αν και υπάρχει σημαντική διχογνωμία για το κατά πόσο αυτό έγινε σκόπιμα. Πιο πρόσφατα ο Ούγγρος συνθέτης Bela Bartok και ο Γάλλος αρχιτέκτονας Le Corbusier χρησιμοποίησαν σκόπιμα τη χρυσή αναλογία στα έργα τους. Όμως ακόμα και ο χριστιανικός σταυρός αποτελείται από δύο κάθετες μεταξύ τους γραμμές με την αναλογία ανάμεσα στην κατακόρυφη και την οριζόντια να μην είναι άλλη από τον αριθμό φ.
Ακόμη και σήμερα η χρυσή αναλογία απαντάται σε πλήθος αντικείμενα φτιαγμένα από τον άνθρωπο. Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα το σχήμα της οποίας είναι ακριβώς αυτό.
Οι πολυάριθμες εμφανίσεις της χρυσής αναλογίας, και των χρυσών ορθογωνίων στην τέχνη, είναι αντικείμενο συζητήσεων και ερευνών μεταξύ των ψυχολόγων για το κατά πόσο οι άνθρωποι αντιλαμβάνονται το χρυσό ορθογώνιο για παράδειγμα, ώς πιο όμορφο και αρμονικό σχήμα από οποιοδήποτε άλλο ορθογώνιο. Το 1995 ο καθηγητής Christopher Green του Πανεπιστημίου York στο Toronto, σε ένα άρθρο του στο περιοδικό Perception παρουσιάζει τα αποτελέσματα μιας σειράς πειραμάτων που δεν έδειξαν κάποια μετρήσιμη προτίμηση για το χρυσό ορθογώνιο, δεν παραλείπει όμως να αναφέρει ότι αρκετοί άλλοι συνάδελφοί του έχουν αντίστοιχα δεδομένα που υποδηλώνουν ακριβώς το αντίθετο, ότι δηλαδή υπάρχει μια τέτοια τάση.
Πέρα όμως από τα επιστημονικά δεδομένα η χρυσή αναλογία, ο αριθμός φ, περιβάλλεται από ένα πέπλο μυστηρίου, κυρίως γιατί εντυπωσιακές προσεγγίσεις του απαντώνται, εντελώς απρόσμενα σε ένα σωρό μέρη στη φύση. Ακόμα και μια τομή του ανθρώπινου DNA φαίνεται να ενσωματώνεται άψογα σε ένα χρυσό δεκάγωνο. Η χρυσή αναλογία και τα σχήματα που σχετίζονται με αυτή συνεχίζουν να κινούν το ενδιαφέρον των μαθηματικών, αλλά και των απλών ανθρώπων.
Πηγή: Άρθουρ Μπέντζαμιν: Η μαγεία της ακολουθίας Φιμπονάτσι


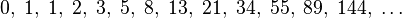

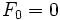 και
και  .
.